Escuela hispánica de dirección de orquesta
Vicente Chuliá, Curso de dirección de orquesta
11. Análisis de las partituras musicales
2b. Glomérulos constituidos por periodicidades de compases
Introducción - 14 julio 2019
Periodicidades isomorfas - 25 julio 2019
Periodicidades contraídas y dilatadas - 27 julio 2019
Periodicidades entrelazadas e interrumpidas - 29 julio 2019
Periodicidades mutadas y transformadas - 31 julio 2019
Glomérulos constituidos por periodicidades de compases: introducción
Vicente Chuliá FMM 047 (32' 21'')
Introducción
Una vez entendido que una aglutinación de sonidos ordena, agrupa y mide la música por medio de las figuras geométricas y sus puntos (FMM 046), es el momento de plantear un estudio profundo y denso sobre las periodicidades que generan los glomérulos a distinta escala y que permiten la expansión de la construcción musical.
En el libro Fraseo musical de Hugo Riemann, el autor explica los conceptos tradicionales de “antecedente” y “consecuente” en música que tienen lugar a partir de la reagrupación de los motivos en un grupo de compases si bien Riemann los engloba bajo la idea musical de “Frase” recogida de Juan Abraham Peter Schulz:
«En la Teoría de las Bellas Artes (1772) de Sulzer, se encuentra con el título “Interpretación Musical”, un artículo publicado por el conocido compositor Johann Abraham Peter Schulz. En este artículo aparece por primera vez, en la literatura teórica alemana, la palabra frase, usada para indicar cada miembro de una melodía que por sí mismo forma un período bien determinado. Al crear este término, el autor cree necesario acompañarlo de una nota explicativa: “Tomo aquí la palabra frase en su sentido más amplio, de modo que se comprendan en ella tanto los incisos como las cesuras y los periodos del canto. Estas divisiones diversas las indicaré todas de un mismo modo. En realidad, los grandes intérpretes hacen notar a veces en ellos pequeños matices, pero tan sutiles y difíciles de señalar que me limitaré a la sola indicación antedicha”.»{1}
Sobre esta premisa, Riemann constituye un estudio interpretativo sostenido por un análisis sistemático de las periodicidades de compases que, según él, deben recalcarse interpretativamente mediante incisos y pequeñas cesuras que articulen correctamente el discurso sonoro. Así pues, a partir de este principio analítico introducido por Riemann, en la institución musical comienzan a publicarse centenares de libros de análisis musical donde aparecen un conjunto de términos e ideas entrelazadas de forma confusa y oscura como puedan ser “Período”, “Frase”, “Motivo”, “Tema”, “Elemento”, &c., cuyos significados varían en tanto que varían los autores de cada tratado musical. Con esto no negamos que la repercusión analítica concurrida en este contexto histórico no fuera positiva, sino que sostenemos la tesis de que la confusión que tuvo lugar debido a tal polisemia de términos no vino por parte de un error interpretativo de dichos autores, sino por una debilidad ontológica del propio sistema de Riemann del cual partió todo.
En consecuencia, y para poder aportar lucidez a este embrollo terminológico que no hace más que deslizar el estudio analítico de las partituras hacia un formalismo musical, nos ceñiremos, en primer lugar, a recorrer la historia de las operaciones musicales objetivándolas a partir de dos géneros existentes en la escritura compositiva, a saber; el género melódico y el género contrapuntístico. Estos dos géneros no son disyuntos ni separables, sino que mantienen continuas intersecciones que deben ser tratadas a partir de una interpretación lógica de la evolución histórica de la composición musical.
Partiendo del canto gregoriano observamos que la línea que conduce el discurso de esta música está basada en un canto melódico (melismático realmente) en el cual se establecen identidades a partir de dos prismas, a saber, la identidad fenoménica de los modos y la identidad melismática del dibujo melódico (línea), luego aquí yace la génesis del género melódico por antonomasia, y a este deberían de acercarse todos los músicos que pretendan entender el significado de melodía y su asociación con la poesía (aeide = cantar; aw = hablar).

Imagen 1. Primera fase: cantus firmus
La siguiente fase evolutiva de la escritura musical la obtenemos en el Organum. Aquí nos encontramos con la génesis del punctum conta punctum si bien el punctum que va a la contra no desdibuja la fisonomía del cantus firmus (melódico), por lo cual, el género, aunque transformado, se sigue manteniendo como melódico.

Imagen 2. Segunda fase: Organum
En la tercera fase, en cambio, objetivada entre el Ars Antiqua, Ars Nova y polifonía renacentista, ya tiene lugar una transformación sin precedentes, a saber; la gran contradicción que se halla entre las voces (movimientos contrarios, movimientos en espejo, movimientos en rotación y traslación...), así como el aumento de cantidad de estas, hace que la identidad fenoménica y el dibujo lineal del cantus firmus sea desdibujado de tal forma que ya no permite que se establezca a partir de él ninguna identidad siendo la nueva identidad resultante procedente de la propia fragmentación de elementos contrapuntísticos más pequeños que serán imitados, contrapunteados, extendidos, modulados, invertidos, &c. Aquí yace el origen de los denominados “Motivos”. El motivo, será en esta música la materia sobre la que, yendo de un estrato a otro así como conjugándose todos a la vez, se desarrolle la obra. Esta es la esencia del género contrapuntístico, el género principal de la evolución musical que es estudiado en el “Contrapunto severo” o “Contrapunto de escuela”.

Imagen 3. Tercera fase: contrapunto florido
En la cuarta fase evolutiva de la música, contextuada entre el Barroco y el Clasicismo (con la constitución de la ópera, el bajo continuo, el desarrollo musical del luteranismo en corales, el estilo galante, &c.), se lleva a cabo la búsqueda de la melodía como el “alma” de la música (Rousseau). Ahora bien, siendo cierto que el género melódico del Barroco y Clasicismo ha dado posibilidades de extensión modulante a la música, ¿qué sería de este género sin la elaboración de dichas melodías y sus desarrollos constituidos a partir de los principios del contrapunto escolástico? Las elaboraciones (armonizaciones) de estas melodías responden a clases de contrapunto derivados del contrapunto de escuela, como la “contra-melodía” (bajos continuos o contrapuntos que envuelven la melodía principal); el “contrapunto acórdico-rítmico”, el cual acerca la música adjetiva a la sustantiva por medio de los ritmos típicos de las danzas; el “contrapunto cromatofónico” (que dio origen al arte de la orquestación); y las variaciones estatutarias como puedan ser el “contrapunto dodecafónico”, el “contrapunto bitonal o politonal”, y el “contrapunto serial”.

Imagen 4. Cuarta fase: escritura clásica
En función del estudio del curso histórico de la música, definiremos al Motivo como el elemento a extender que puede concurrir de forma contrapuntística o melódica; el Sujeto será la extensión del motivo que se tratará dentro del género contrapuntístico; y el Tema el material que se extiende a partir del género melódico pudiendo expandirse posteriormente con mezcla entre ambos géneros. El Periodo, pues, será el orden, organización y cohesión por el cual el Motivo, Sujeto o Tema se circunscriben operatoriamente a uno de los géneros identificados. La idea de Frase, en cambio, la situaremos sólo en un ámbito análogo perteneciente al mundo de la ejecución con la función de indicar una maestría de oficio en el articular de los periodos.
Desde la filosofía materialista de la música, la idea de Período se concibe como una unidad holomorfa, a saber:
«Desde la perspectiva “trivial” del Ars Dicendi tradicional, el concepto que hemos podido encontrar más afín a las “unidades holomorfas” ha sido el concepto de periodo. José Kleutgen (1811-1883), que cita como denominaciones diversas [conónimas] de periodo, dentro del vocabulario de Cicerón, a las siguientes: ambitum, circuitum, comprehensionem, circunscriptionem, define el periodo de este modo […] y supone que a la formación de un periodo concurren tres condiciones: (1) una cierta amplitud de la oración, (2) la copulación de sus partes, y (3) el número, porque el periodo es una “oración numerosa”. Y como parte del periodo –por tanto, como partes de la “cadena”– Kleutgen cita a los miembros (kolon), a los incisos (kommata), a la prótasis (antecedente) y a la apódosis (consecuente), que dividen el periodo en dos partes. También distingue Kleutgen dos géneros de periodo: el simple (monocolos) –que puede sin embargo tener incisos–, el bimembre (prótasis, apódosis), el trimembre, el tetramembre (tres prótasis y una apódosis, o una apódosis y tres prótasis). Por otra parte, los periodos pueden amplificarse o comprimirse.»{2}
Para estudiar las periodicidades musicales, este criterio sería insuficiente si no se completara con un riguroso estudio de los contextos determinados y de los esquemas materiales de identidad de las obras.
Las construcciones categoriales se mantienen en un ámbito de términos, relaciones y operaciones, esto es, los puntos y rectas en Geometría, las distancias o la adición, pero a partir de estos términos no se podría construir ninguna ciencia si no fuese por las morfologías y construcciones que de ellas se derivan, es decir, circunferencia, cuadrado, triángulo... Estas configuraciones morfológicas en cuanto a principia media son los contextos determinados. Estos contextos son la primera fase por la cual pueden desarrollarse unas relaciones que los justifiquen como una verdad (identidad sintética sistemática) por medio de teoremas que constituirán el cierre de la propia categoría siendo esta segunda fase la que corresponda a los contextos determinantes. En música, podemos hablar de contextos determinados, esto es, leyes contrapuntísticas, armónicas, de morfología en la instrumentación, de afinación, &c., pero estos parten de normas mutables a lo largo de la historia, a saber, prohibición de intervalos de cuarta en tiempos fuertes, quintas seguidas, duplicación de sensible... de modo que (y aquí yace la razón principal de que la música no es ciencia) no pueden constituirse como contextos determinantes. Gustavo Bueno lo explica a partir de una crítica al paradigma de Kuhn, según la cual la idea de paradigma se circunscribe a la de contextos determinados y contextos determinantes, es decir, las armaduras cambiantes según la época que son comunes en las ciencias, así como en otras instituciones como pueda serlo la música, constituirían contextos determinados que no serían determinantes. Así pues, el problema de la idea de Paradigma es que no distingue los elementos de la ciencia que derivan en identidades sintéticas sistemáticas (distinción entre contextos determinados y determinantes). En este sentido, los contextos determinados en música son tanto los sistemas por los cuales se produce la obra musical (modalidad, tonalidad, bitonalidad, politonalidad, dodecafonismo, serialismo...) como los modelos operatorios (fuga, minueto, suite, sonata, cuarteto, sinfonía...) que sirven como ente racional de la enseñanza teórica y que funcionan como un anamnesis-prolepsis. Estos contextos determinados conforman en cada obra unos esquemas materiales de identidad a partir de los cuales se expande el compuesto musical en glomérulos a distinta escala:
«El esquema material de identidad podría hacerse corresponder con la causa material aristotélica, siempre que ella quedase determinada según criterios positivos E, que expresamos por la fórmula E(H). El efecto se define entonces como una interrupción, ruptura, alteración o desviación del esquema material procesual de identidad (ruptura que no afecta, en principio, al sistema que, por decirlo así, engloba al efecto). Se comprenderá, dada la relatividad del concepto de efecto, no ya inmediatamente a su causa, sino a un esquema material procesual de identidad (dado en un sistema complejo de referencia) que, si no es posible determinar en cada caso este esquema procesual de referencia, la noción de efecto se desvanece.
De aquí se sigue que la idea de creación o de efecto creado es absurda o vacía puesto que en la creación el único esquema de identidad que cabe ofrecer es la nada (creatio ex nihilo subiecti) –y no la causa eficiente divina inmutable– es decir, justamente lo que no puede ser un esquema de identidad.»{3}
Los esquemas materiales de identidad en Música están concatenados a los contextos determinados. Son sistemas complejos, materiales y procesuales configurados y formados por estos contextos determinados que se toman como modelo. Así pues, entendemos que los esquemas materiales de identidad son el punto de referencia o la razón –que no causa– de una obra musical. A partir de estos esquemas no podemos referirnos a la expresión “causa-efecto”, ya que el efecto se define como alteración o desviación si bien la relatividad del concepto Efecto no es a su Causa, sino al esquema material de identidad. Es decir, que toda la concatenación y evolución procesual que toma unos cauces lógicos sin los cuales no habría música sino una “algarabía sonora”, están cimentados sobre estos esquemas materiales.
En consecuencia, para establecer un criterio analítico en música desde el materialismo filosófico, debemos aclarar que el género de escritura más complejo y complexo de la institución musical es el “género mixto” (la mezcla entre los géneros melódico y contrapuntístico ya expuestos). Por lo tanto, el proceso de elaboración de una obra musical debe ser analizado a partir de una analogía de atribución con las ciencias positivas que puede ser ciertamente muy útil para precisar los esquemas materiales de identidad y su expansión en el compuesto. Trataremos los distintos estromas que conformen las periodicidades musicales a partir de términos, relaciones y operaciones constituyendo, así, los siguientes términos que conformarán las especies de glomérulos que irán constituyendo las distintas generaciones basadas en las periodicidades de compases:
- Términos métricos
- Términos melódicos
- Términos contrapuntísticos
- Términos acórdicos
- Términos cromatofónicos
Notas
{1} Hugo Riemann, Fraseo musical, 2ª ed., Nacional, México D.F., 1958, pág. 13.
{2} Gustavo Bueno, “Poemas y Teoremas”, El Catoblepas, junio 2009, nº 88, pág. 2.
{3} Pelayo García Sierra, Diccionario filosófico. Manual de materialismo filosófico (1999), 2ª ed., versión 3 (2018), en Proyecto Filosofía en español, s.v. “Efecto (concepto de) / Esquema material procesual de identidad”.
Glomérulos constituidos por periodicidades de compases: periodicidades isomorfas
Vicente Chuliá FMM 048 (23' 33'')
Glomérulos constituidos por periodicidades isomorfas
Para comprender lógicamente la estructura de una obra musical (como totalidad atributiva) se deben establecer unos principios que por su propia reiteración operatoria (isos = igual; morphe = forma) concurran discursivamente en una solidez (identidad) constructiva.
El isomorfismo se establece en función de las especies métricas, melódicas, contrapuntísticas, acórdicas y cromatofónicas, que conforman los términos musicales, y pueden concurrir a distinta escala menores o mayores a una periodicidad, esto es, desde el eje X obtenemos los isomorfismos métricos; desde el eje Y los isomorfismos melódicos que dan lugar, en caso de no haber un estrato prioritario, a isomorfismos contrapuntísticos y acórdicos; y desde el eje Z obtenemos los isomorfismos cromatofónicos.
A lo largo de la historia de la institución musical, se han conceptuado los isomorfismos en tratados dentro del apartado de los estudios contrapuntísticos dedicado a la “Imitación”. En este sentido, utilizaremos como base la clasificación de Hilarión Eslava ampliada y actualizada por el propio desarrollo de la idea de Glomérulo, a saber:
- Paso o antecedente que va a ser imitado
- Imitación de sólo ritmo
- Imitación de ritmo y dirección de movimientos de las voces (ascendente o descendente)
- Imitación de ritmo e intervalos (aunque exista mutación de tonos y semitonos)
- Imitación de intervalos, tonos y semitonos
- Imitación de ritmo, intervalos, tonos y semitonos
- Imitación por movimiento contrario
- Imitación por disminución
- Imitación por aumentación
Sobre esta clasificación desarrollaremos las periodicidades si bien disociando aspectos que, aunque inseparables del principio identitario por la reiteración operatoria (imitación), funcionan desde especies terminológicas distintas:
1. El género isomorfo se referirá al motivo o paso desde el cual se desarrollarán los periodos de compases mediante una imitación severa, y esta se estudiará desde las especies comunes a todos los géneros (isomorfismos, contracciones y dilataciones, entrelazamientos e interrupciones, y mutaciones).
2. La imitación de sólo ritmo o de sólo intervalos, tonos y semitonos a la que se refiere Eslava, será un isomorfismo que podrá ser desarrollado en cualquiera de las diferentes especies.
3. La imitación por disminución o aumentación, por movimiento contrario o por mutación, se estudiarán en los géneros constituidos por contracciones, dilataciones y mutaciones.
4. Los géneros y especies pueden entremezclarse, entrelazarse o interrumpirse. Este tipo de procedimientos se estudiarán en el género de periodicidades entrelazadas o interrumpidas.
Isomorfismos métricos
La música sustantiva está basada en sonidos muy elaborados y sofisticados por la razón, por lo que su ritmo no es “natural” como el ritmo que hacían los hombres de las cavernas, sino que se basa en el movimiento musical. La ordenación de los ritmos por medio de un medir racional es lo referido a la métrica. Métrica es, pues, lo relativo a la estructuración del ritmo medido del movimiento musical a través de la unidad del compás:
La métrica es al ritmo, lo que el reloj al tiempo y el termómetro a la temperatura. El reloj mide el tiempo, pero no es el tiempo; el termómetro mide la temperatura, pero no es la temperatura. Cuando ritmo y métrica van asociados, aquél representa el contenido; ésta, el continente.{1}
A continuación pueden observarse unos cuantos ejemplos de isomorfismos métricos:


Ejemplo 1. Sinfonía nº 7, L. V. Beethoven


Ejemplo 2. Sinfonía nº 5, L. V. Beethoven

Ejemplo 3. Canción popular

Ejemplo 4. Capricho nº 24, N. Paganini

Ejemplo 5. “Bolero”, M. Ravel
Isomorfismos melódicos
Cuando la línea melódica (bien comprimida en motivos, sujetos o temas) es reiterada, nos encontramos con un isomorfismo melódico. La melodía, tal como explica E. Toch, necesita de unos patrones métricos para ser estudiada como tal, pero esta inseparabilidad de metro y melodía no arrastra una imposibilidad de disociación. Así pues, el estudio de los isomorfismos melódicos puede establecerse a partir de distintas fisonomías de la melodía, a saber, líneas rectas ascendentes o descendentes, ondulaciones conformadas por líneas curvas, los movimientos angulares y las mixturas. Por ejemplo, los floreos, las bordaduras, las escapadas, los retardos, las apoyaturas, etc., permiten que se comprenda la propia constitución del desarrollo melódico.
Como se puede comprobar en el ejemplo 4, muchas veces el isomorfismo métrico y melódico concurren simultáneamente. A continuación, véase un ejemplo melódico-isomorfo:
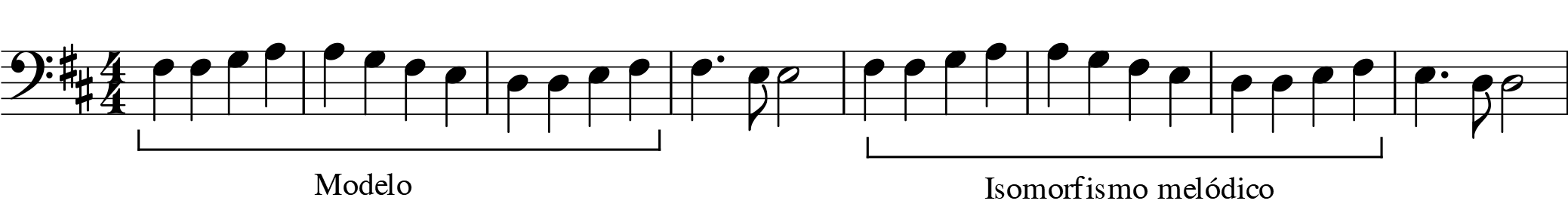
Ejemplo 6. Sinfonía nº 9, L. V. Beethoven
Isomorfismos contrapuntísticos (contrapunto trocado o invertible)
La acepción más general que corresponde en la escolástica compositiva al isomorfismo contrapuntístico es el concepto de “Imitación”, ya que este no es una simple repetición organizada como expansión melódica sobre una sola voz, sino que el propio concepto encierra en sí una diversidad de estromas sonoros que van sucediéndose jerárquicamente en la importancia identitaria plasmada sobre el propio isomorfismo de la imitación.
Nos referiremos a isomorfismo contrapuntístico (lisológicamente) cuando esta imitación sea llevada a un complejo despliegue lógico operacional plasmado a partir del tradicional contrapunto trocado o invertible. Ahora bien, cuando esta imitación sea más “libre” o cuando corresponda con una propia extensión periódica, se analizará desde otros géneros y especies, ya que su propia dialéctica nos conduce a conformaciones más symploké que no se enclaustran exclusivamente dentro de los isomorfismos contrapuntísticos, como por ejemplo en los divertimentos de las fugas.
Así pues, los contrapuntos invertibles a cuatro voces se constituyen a partir de los elementos A-B-C-D, los cuales prosiguen desde la inversión sin alterar las propias normas de las que parten. Véase el siguiente ejemplo de isomorfismo contrapuntístico del autor Manuel Massotti Littel:

Ejemplo 7. Tratado Apuntes de Contrapunto y Fuga (inéd.), M. Massotti
Isomorfismos acórdicos
La vinculación del concepto de acorde (accordare =“ir hacia el corazón”) con la idea de Armonía (armós = “juntar una cosa con otra”, “hombros”), se circunscribe directamente por su propia relación etimológica. “Acordar” y “juntar” son dos caracteres operatorios que en música parecen divergir de “contrapunto”, que posee un elemento significativo de discordancia entre varias confluencias sonoras.
Tradicionalmente, en los tratados escolares se ha hablado de la armonía como el estudio de la correlación y entrelazamiento de varios acordes. Sobre este asunto debemos hilar muy fino en nuestro análisis. Bien es cierto que el entrelazamiento de un conjunto de acordes desde sistemas constituidos a priori (a partir de postulados estéticos y antropológicos) responde a una idea de armonía, pero ¿no ocurriría lo mismo con el entrelazamiento, correlación y conexión de confluencias rítmicas objetivadas y ordenadas mediante patrones métricos? ¿No sería cierto que el entrelazamiento de melodías, en su peculiaridad expansiva necesaria para el arte musical, responde también a una idea de armonía? ¿No sería aún más cierto que lo que responde a una idea general de armonía en música reside en el entrelazamiento (armós = juntar) de todos estos elementos terminológicos?
En muchos libros de análisis musical pueden apreciarse conceptos como “ritmo armónico”, “ritmo melódico”... siendo que ritmo y armonía no responden a conceptos sino a ideas, a diferencia de contrapunto, acorde o instrumentación, que sí responden a conceptos debido a su encasillamiento a una sola categoría. Ritmo y armonía, en cambio, son las ideas que hacen de puente de transmisión entre las cuestiones constitutivas y las cuestiones de estatuto del arte musical. De esta manera, si el ritmo (atribuimos la idea mayúscula de ritmo a la idea de velocidad expansiva) y la armonía (la conexión –juntar-- de todos los contrapuntos y discontinuidades sonoras) funcionan en una obra musical, consideraremos a esta obra como una composición bien construida que puede analizarse desde distintos ámbitos. Así pues, debe estudiarse, en esta especie de isomorfismo, las identidades acórdicas conformadas atributivamente a partir de una distribución de intervalos simultáneos en el tiempo, en relación a las coordenadas tonales de las que forman parte. Por ejemplo, el acorde perfecto mayor o menor, el acorde de séptima de dominante, de séptima de sensible o de séptima disminuida en las tonalidades conformadas por las escalas diatónicas; o el “acorde Tristán”, el acorde de séptima mayor con onceava y treceava, de cuarta aumentada con sexta añadida y séptima mayor en las tonalidades conformadas por la extensión de las escalas diatónicas.


Ejemplo 8
Isomorfismos cromatofónicos
Las cuatro cualidades que conforman el eje Z, presión, intensidad, amplitud y densidad, precisan del
referencial del instrumento, su tesitura, así como de sus posibilidades técnicas. Así pues, la distribución en la instrumentación de un fragmento musical ordenado periódicamente, constituirá una anamnesis cromatofónica que, en caso de que su prolepsis concurra a partir de una repetición idéntica desde esta cualidades instrumentales, constituirá un isomorfismo cromatofónico sin perjuicio de todo tipo de discontinuidades que tengan lugar en las otras especies:

Ejemplo 9. Obertura “Egmont”, L. V. Beethoven
Referencias bibliográficas
Hilarión Eslava. Contrapunto y Fuga, tratado segundo. 2ª ed. Biblioteca Nacional de España, Madrid 1864, pág. 64.
Vicente Chuliá, Manual de filosofía de la música, Pentalfa, Oviedo 2018.
Nota
{1} Salvador Chuliá, “¡Ritmo!, primer elemento de la música”, Ruta, Sociedad Cultural ABC, Catarroja 1981.
Glomérulos constituidos por periodicidades de compases: periodicidades contraídas y dilatadas
Vicente Chuliá FMM 049 (29' 28'')
Glomérulos constituidos por periodicidades contraídas y dilatadas
En la presente lección, se continua desarrollando la Teoría de los glomérulos musicales desde la referencia de los esquemas materiales de identidad que se explicaron en la lección introductoria a esta clase de glomérulos constituidos por periodicidad de compases (FMM 047). Desde esta referencia, las periodicidades que trataremos en la presente lección corresponden con el género de contracciones y dilataciones.
Contracción viene del latín contractio y se refiere a la acción y efecto de contraer (estrechar, juntar, encoger); en cambio, Dilatar (del latín dilatare) se refiere a extender, alargar y “hacer mayor una cosa”. En música uno de los recursos compositivos más importantes que existen para posibilitar la expansión, desarrollo y evolución de una obra es la contracción y dilatación de la dialéctica sonora que genera forma y materia a partir de los tres ejes del volumen musical por medio de su organización periódica. Tomamos, pues, la funcionabilidad de estas palabras desde los antecedentes siguientes, a saber, en los tratados escolásticos de contrapunto y fuga, cuando se trata el contrapunto canónico, se clasifican los cánones en regulares, irregulares, retrógrados, en espejo o movimiento contrario y por ampliación o por disminución. Otros tratados, como por ejemplo el tratado inédito de contrapunto y fuga de don Manuel Massotti Littel –entre otros–, utilizan las ideas de contracción y dilatación en lugar de ampliación y disminución. Aunque para el caso del canon o contrapunto imitativo, la aumentación y disminución significan lo mismo que la dilatación y contracción, en el caso que nos ocupa, la distinción es de suma importancia. La ampliación o disminución se refiere a un material de construcción compositivo que se expande a través de isomorfismos melódicos que, en este caso, son a dobles –o más– valores métricos (ampliación), o a mitad –o menos– valores métricos (disminución). No obstante, cuando hablamos de dilatación o contracción, en el aspecto que estamos tratando (es decir, periodicidad de compases), implican un desarrollo que, si bien parten de isomorfismos, son una extensión (dilatación) o contracción de los elementos identificados (identidades). Sobre la distinción entre “extensión” y “dilatación” debemos remitirnos al libro del musicólogo Ralph Kirkpatrick sobre Dominico Scarlatti. En este libro hay un apartado dentro del capítulo de análisis armónico al que llama contracciones y extensiones. El problema de no contraponer a “contracción” su lógico antónimo “dilatación”, acarrea problemas ontológicos en el análisis, a saber; la contraposición de los conceptos contracción-extensión supone –o puede dar a entender– que la contracción no puede producir una extensión, en cambio, el mismo Kirkpatrick se contradice explicándonos lo siguiente:
«Esta contracción de las fórmulas cadenciales es uno de los principales métodos de Scarlatti para variar el movimiento armónico dentro de una pieza. Las cadencias pueden ser amplias y expandirse al final de la obra.
Sus elementos pueden contraerse o velarse en el centro en los pasajes modulatorios, o convertirse en secundarias de armonías creadas por el movimiento diatónico. Cuando Scarlatti acelera las cadencias, los elementos pueden aparecer tan amontonados que dan pie a una llamada acciacatura, al igual que las aspas de una hélice que se mueven a gran velocidad.»{1}
Si analizamos rigurosamente esta cita, observamos que una contracción puede expandirse y extenderse, por lo que se debe discernir la extensión (expansión) –siempre necesaria en música y llevada a cabo por el ingenio dialéctico del compositor– de la propia contracción o dilatación de los elementos materialmente desarrollados.
Contracción-Dilatación métrica
La métrica, como ordenación racional y objetivada del ritmo, constituye, en las periodicidades, un componente identitario que puede efectuarse desde distintos movimientos así como por dilatación o contracción. Véase a continuación el siguiente ejemplo de contracción y dilatación métrica:

Imagen 1. Término métrico simple A
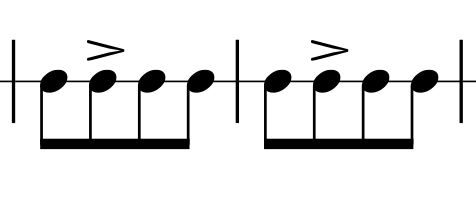
Imagen 2. Término métrico simple B
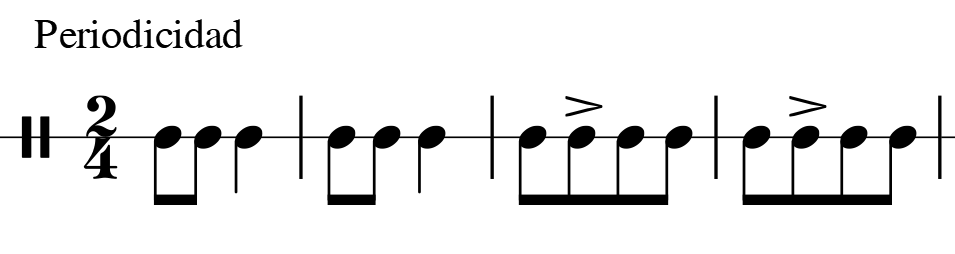
Imagen 3. Término métrico compuesto conformado por los términos simples A y B (esquema material de identidad métrico)
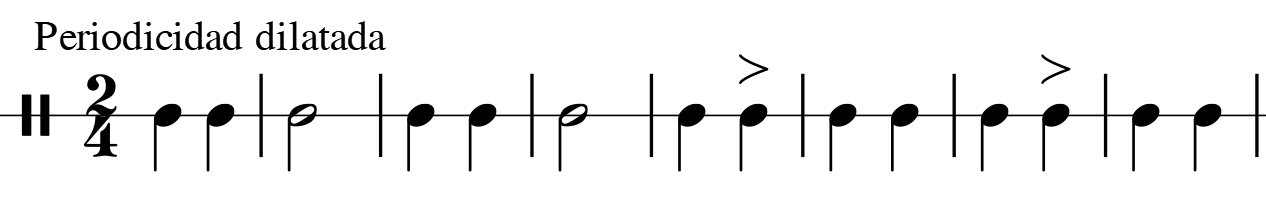
Imagen 4. Dilatación del esquema material de identidad métrico

Imagen 5. Contracción del esquema material de identidad métrico
Contracción-Dilatación melódica
Si bien la contracción o dilatación métrica puede –no en todos los casos– arrastrar una contracción o dilatación melódica, el aspecto melódico es disociable del métrico. Sobre esta cuestión queremos explicar como ejemplo material de este tipo de contracción y dilatación, el elemento operatorio más decisivo en la construcción del primer movimiento de la Quinta Sinfonía de Beethoven.
Observando las cuatro notas temáticas que inician el movimiento de la Sinfonía (Sol-Mib-Fa-Re), nos damos cuenta de que en este zigzag melódico el intervalo de tercera es un componente que, al repetirse en progresión descendente (Sol-Mib modelo; Fa-Re 1ª repetición en progresión descendente), crea un isomorfismo melódico de traslación en el eje Y. Además, si analizamos con mayor meticulosidad, vemos que sobre el Mi bemol hay un calderón por lo que esta nota adquiere gran importancia junto con el Re sobre el cual está situado otro calderón (en el siguiente isomorfismo trasladado) aunque esta vez extendiéndolo a un compás más; es decir, que la importancia que el “ojo” del calderón nos hace ver recae sobre la relación entre Mib-Re: un semitono.

Imagen 6. Esquema material de identidad

Imagen 7. Identidad conformada por semitono

Imagen 8. Identidad conformada por un movimiento en zigzag de terceras
Por lo tanto, tenemos: el esquema material de identidad formado por Sol-Mi bemol (con calderón), y traslación isomorfa Fa-Re (con extensión del Re y calderón), es decir, una dilatación del segundo subperiodo, mas ¿cómo se desarrolla este tema? Pues bien, en la primera periodicidad vuelve a aparecer el Sol-Mi bemol, pero en vez de en posición de tercera descendente, en sexta ascendente –rotación o inversión de la tercera– y el semitono de Mi bemol-Re que es trasladado discursivamente a La bemol-Sol haciendo que la sexta se constituya a través de una dilatación de dos a cuatro compases continuando con cuatro compases más que buscan un Fa-Re también por medio del La bemol-Sol.

Imagen 9. Dilatación melódica conformada por la rotación de la 3ª en 6ª a través del semitono trasladado
A continuación (compás 15 con anacrusa) la música se desenvuelve a partir de una repetición isomorfa –con imitaciones regulares contraídas– que se dilata a una periodicidad de 7 compases. Tratemos el asunto con rigor; la primera gran periodicidad se compone de 2+3 compases, es decir, 5 compases (imagen 6); la segunda se compone de 4+4 compases, o sea 8; y la tercera, de 7 compases hasta llegar a una quinta ascendente donde reside otro calderón. Total de compases: 15 (8+7). Así pues, si nos percatamos bien de esta forma de operar, nos damos cuenta de que la asimetría es aparente puesto que reside en lo local. Los cinco compases de la primera periodicidad, conformados a partir de dos subperiodos donde el segundo es una extensión del primero (primer subperiodo, 2; segundo subperiodo, 2+1), están relacionados con la asimetría existente entre el segundo gran periodo y el tercero, a saber; el segundo gran periodo consta de 8 compases y el tercero de 7. Ahora bien, en este último compás (compás 21) se encuentra un calderón que prolonga la nota el doble de su valor, es decir, que la “dobla” en dos compases más. La conclusión es que no son 7 compases sino 9 (8+1). El fundamento por el cual atribuimos la técnica de la dilatación melódica al desplegar de esta pieza es el siguiente: la analogía entre la extensión del segundo subperiodo de la primera gran periodicidad (2+1) y la segunda gran periodicidad respecto a la tercera (8+1).
La segunda periodicidad está formada por 8 compases (4+4), simétricos a los 8 compases del principio de la primera periodicidad. Esta periodicidad continua a partir del mismo procedimiento operatorio de dilatación melódica en el que se desarrollaba la segunda parte de la primera periodicidad, ahora bien, dilatando todavía más (a través de contracciones métricas) respecto a la primera periodicidad, a saber: segunda parte de la primera periodicidad 7+2=9; segunda parte de la segunda periodicidad 9+2=11.
La última gran periodicidad se inicia con un vector producido por el final de la segunda parte de la segunda periodicidad. Esta tercera periodicidad está conformada por 15 compases que son simétricos a los 5 compases que componen el esquema material de identidad de la obra, así como a las tres periodicidades dilatadas que conforman el tema A y su desarrollo del primer movimiento de la Sinfonía: 3×5=15.
Como conclusión ante este análisis podemos delimitar que una esencia dialéctica plagada de contraposiciones (asimetría local, contracción y dilatación de elementos) es completada sobre una simetría a mayor escala que emerge de un tejer de “hilos” contradictorios confeccionados a partir del ingenio del compositor y fuera de cualquier a priori operatorio (más que el propio oficio y técnica) del trabajo.

Imagen 10. Esquema del análisis de las dilataciones concurridas en el principio del Primer movimiento de la Quinta Sinfonía de L. V. Beethoven
Contracción-Dilatación contrapuntística
Reafirmándonos en que la esencia de la operación musical reside en el contrapunto, utilizaremos el criterio clasificatorio de las especies de J. Fux para poder objetivar la idea de contracción o dilatación contrapuntística. Al respecto debemos analizar el sentido operatorio de las especies desde el punto de vista de los glomérulos constituidos por periodicidades que conforman contracciones o dilataciones:
— Primera especie. Esta especie, a grandes rasgos, constituye la esencia del acorde (nota contra nota) siempre y cuando el contrapunto sea a tres o más voces. Ahora bien, ¿dónde estriba el límite entre el acorde y el contrapunto siendo que el primero parte de la primera especie del segundo? Debemos deslindar rigurosamente este delicado asunto a partir de un análisis distributivo y otro atributivo, a saber, para empezar, consideraremos, lisológicamente, a cada punto como una totalidad distributiva que, a su vez, constituye una parte de la totalidad atributiva; a ésta la analizaremos desde dos criterios: la simultaneidad sonora de los puntos (estroma acórdico) y el conglomerado operatorio de las periodicidades melódicas (contrapunto). Aquí yace la aclaración de la anterior cuestión que demuestra la inseparabilidad pero disociación entre los términos acórdico y contrapuntístico.
La contracción y dilatación contrapuntística que enuncia esta especie se halla precisamente en el segundo criterio de atribución, a saber, al igual que en una barca de madera, las tablas expuestas al calor se dilatan ocasionando pequeños espacios entre éstas mientras que con el frío se contraen y, por ende, se cierran dichos espacios, todo contrapunto que concurra en oposiones interválicas/melódicas respecto al cantus firmus, constituirá una divergencia (dilatación de las tablas por el calor) siendo el caso contrario (contrapunto en paralelo al cantus firmus) una convergencia (tablas contraídas por el frío). Las principales leyes de la divergencia, históricamente, se constituyeron a través del contrapunto severo o de escuela a partir de la contradicción del Organum establecida por el Discantus donde lo que se trataba era de establecer las siguientes reglas, a saber: prohibición de quintas seguidas; prohibición de tres o más sextas seguidas; prohibición de disonancias (cuartas, segundas, séptimas, novenas, intervalos aumentados o disminuidos, &c.) sin preparar; así como la búsqueda de la divergencia de movimiento entre las voces. A continuación podemos observar un claro ejemplo de contracción y dilatación contrapuntística:

Imagen 11. Contracción contrapuntística

Imagen 12. Dilatación contrapuntística
— Segunda especie. Al ser dos notas contra una, el cantus firmus se desarrolla al doble métrico que el contrapunto, ofreciendo una herramienta de expansión al compositor desde dos prismas, saber; el devenir melódico del contrapunto y la posibilidad de ejercer isomorfismos melódicos que, al moverse en dos metros diferenciados, producen una dilatación en las voces que se desarrollan como cantus firmus o nota contra nota respecto a los contrapuntos que enuncian dichos isomorfismos en una característica basada en la evolución (expansión) melódica.
— Tercera especie. En este caso, las posibilidades de contraste aumentan, ya que la proporción 4/1 hace que el contrapunto se pueda analizar de manera más clara desde términos melódicos, por lo que este aumento de notas por compás puede enfatizar un recurso compositivo conformado por la ya analizada contracción melódica. Esta manera de proceder puede establecer unas identidades melódicas en el cantus firmus que ya se dejen oír antes por el contrapunto de manera contraída (también en la 2ª especie puede darse, pero naturalmente al ser ésta de contraste métrico menor, se percibe más como dilatación que como contracción) desarrollándose y evolucionando melódicamente.
— Cuarta especie. Este es el recurso de dilatación por antonomasia. La suspensión (retardo) de la nota del contrapunto respecto al cantus firmus “empuja” la música o bien la cimienta a partir de un aumento de densidad que hace que esta voz contrapuntística esté llena de vigor expansivo.

Imagen 13. Contrapunto contraído (sin dilatación por cuarta especie) de primera especie

Imagen 14. Contrapunto dilatado por cuarta especie
— Quinta especie. Al ser esta especie una mezcla de las anteriores produce grandes posibilidades dialécticas de contrastes en la velocidad expansiva del discurso musical. El propio floreo de las voces sienta las herramientas operatorias que permiten producir identidades que por medio del isomorfismo puedan ser contraídas y/o dilatadas.
— Contrapunto imitativo. Aunque la imitación ha sido tratada en los glomérulos constituidos por periodicidades isomorfas, ésta constituye uno de los ejemplos más sólidos de la escritura musical cuando es dilatada o contraída contrapuntísticamente. La imitación está institucionalizada en los estudios del contrapunto imitativo y fuga. Véase el siguiente ejemplo:

Imagen 15. Canon a la 5ª por contracción

Imagen 16. Canon al unísono por dilatación

Imagen 17. Canon a la 8ª por dilatación
El contrapunto imitativo plasmado en la fuga aparece desarrollado de forma contraída y dilatada en los procedimientos de estrechos (contracción) y de pedal de dominante (dilatación), los cuales ejercen la función de asimilar las contradicciones ejercitadas a lo largo de la fuga.
Contracción-Dilatación acórdica
Desde las premisas explicadas en la lección dedicada a los isomorfismos acórdicos (FMM 048), consideraremos una dilatación o contracción acórdica a los siguientes casos, a saber:
— Cuando un acorde constituido por “notas contra notas” (en sentido vertical) tenga una relación métrica simultánea entre las voces y que, al constituirse como identidad (acórdico-métrica), sea reiterado isomórficamente. En este punto debemos aclarar la diferencia entre considerar una periodicidad basada en isomorfismos acórdicos o considerarla como una contracción o dilatación acórdica, y para ello pondremos de ejemplo el primer movimiento de la Sinfonía Heroica de Beethoven. Esta sinfonía comienza con dos acordes en forte de Mi bemol mayor con un corto valor métrico (suenan como dos golpes percusivos); el segundo acorde es un isomorfismo acórdico respecto al primero formando ambos una característica identitaria en la unidad de la obra. Ahora bien, si comparamos estos dos acordes con los acordes de los compases 128, 129, 130 y 131 basados en el acorde de séptima de dominante de Fa (V de la V de la tonalidad principal, por tanto, un movimiento en progressus), podemos observar que, aunque isomorfos, la propia reiteración basada en aquella característica identitaria hace de esta periodicidad –más que de una periodicidad isomorfa– una periodicidad contraída y dilatada. En primer lugar, es contraída debido a que el movimiento métrico en vez de ser ternario (una nota por compás en tiempo fuerte) es binario (comenzando en tiempo débil y emergiendo dos notas por compás); y, en segundo lugar, es dilatada porque se extiende de dos compases (tal como se manifestaba en la identidad del comienzo de la obra) a cuatro compases:

Imagen 18. Esquema material de identidad acórdico de la Tercera Sinfonía de L. V. Beethoven

Imagen 19. Dilatación acórdica de la Tercera Sinfonía de L. V. Beethoven (primer criterio)
— Cuando un conglomerado melódico o contrapuntístico en vez de derivar en una expansión armónica, quede “encerrado” en las coordenadas de un mismo acorde que, contraído o dilatado, emerja y se desenvuelva en un alto grado de densidad expansiva. En el siguiente ejemplo observamos dos compases de dilatación de la dominante de Sol y dos compases de dilatación del acorde de séptima de dominante de Do.

Imagen 20. Dilatación acórdica de la Sexta Sinfonía de L. V. Beethoven (segundo criterio)
— Cuando una combinación acórdica se extiende en traslación isomorfa estableciendo un regressus o progressus. En el siguiente ejemplo (últimos cuatro compases con anacrusas), por medio de resoluciones excepcionales, se extiende la esencia de la característica cadencial V-I por medio de una dilatación de dominantes consiguiendo, con ello, un mayor regressus.

Imagen 21. Dilatación acórdica de la Cuarta Sinfonía de J. Brahms –cuarto movimiento– (tercer criterio)
Contracción-Dilatación cromatofónica
A partir de las coordenadas del eje Z, en cuanto a densidad, presión, intensidad y amplitud que caracterizan a un sonido desde la naturaleza fisicalista del referencial del que parte, estableceremos dos criterios –disociables, aunque inseparables– del binomio contracción-dilatación tímbrica a partir de los cuales ofreceremos intersecciones inevitables con los términos emergentes de los ejes X e Y:
— Criterio distributivo: Basado en el método operatorio de distribuir cada parte (sonido) de una unidad isológica correspondiente a un término musical. Como ejemplo de contracciones o dilataciones procedentes de este criterio podemos citar lo siguiente: pongamos el siguiente caso de contracción de Egmont, donde se conjugan los términos acórdicos perfecto mayor y séptima de dominante en la relación I-IV-V-I. La primera identificación cromatofónica de los dos primeros acordes (compás 82) es conformada por el conjunto de cuerda que será contraído en los dos compases siguientes (compás 84) por el conjunto de viento madera y la trompa, generándose, a partir del compás 92, una dilatación tímbrica que culmina en el compás 99.

Imagen 22. Contracción y dilatación cromatofónica (criterio distributivo)
— Criterio discursivo: Conformado a partir de la relación entre el eje Z y el eje X, es decir, en un análisis más horizontal que vertical. En este sentido hablaremos de dilatación cromatofónica cuando una expansión melódica o motívica sea repartida sobre diversos timbres procediendo, de esta manera, a lo que Schönberg llamaba “melodía de timbres” o Celibidache “continuidad sinfónica”. Por el contrario, contracción consiste en el solapamiento o entretejimiento tímbrico que pueda existir entre esta discursividad dialéctica de los sonidos.

Imagen 23. Dilatación cromatofónica (criterio discursivo)

Imagen 24. Contracción cromatofónica (criterio discursivo)
Referencias bibliográficas
Manuel Massotti Littel, Apuntes de contrapunto y fuga, inéd.
Vicente Chuliá, Manual de filosofía de la música, Pentalfa, Oviedo 2018.
Ralph Kirkpatrick, Domenico Scarlatti, Alianza Musical, Madrid 1985.
Nota
{1} Ralph Kirkpatrick, Domenico Scarlatti, Alianza Musical, Madrid 1985, pág. 198.
Glomérulos constituidos por periodicidades de compases: periodicidades entrelazadas e interrumpidas
Vicente Chuliá FMM 050 (39' 15'')
Glomérulos constituidos por periodicidades entrelazadas e interrumpidas
Entrelazamiento e interrupción son ideas que están íntimamente relacionadas con la idea platónica de symploké (tal y como la entiende Gustavo Bueno desde su rigurosa y potente interpretación de la Historia de la Filosofía) y constituyen el principio esencial de la expansión musical a partir de los metros, alturas, duraciones y cromatofonismos de los sonidos (ejes X, Y, Z). Ahora bien, el contexto por el cual queremos definir y conceptuar la aplicación de la idea de entrelazamiento es muy concreto, a saber, el entrelazamiento glomerular de las distintas periodicidades que conforman los cambios de velocidad expansiva producidos por los progressus, regressus, divergencias y convergencias estudiados en las figuras de la dialéctica (FMM 019). Este criterio ofrecerá las siguientes especies:
Entrelazamientos métricos
Un claro ejemplo de entrelazamiento glomerular métrico de dos secciones aparentemente imposibles de entretejer lo podemos hallar en el desarrollo del tema A y la transición al tema B de la Sonata “Patética” de Beethoven. Los dos temas poseen entre sí una discontinuidad métrica palpable en cuanto a relación de glomérulos constituidos por figuras geométricas (FMM 046), a saber, el tema A se organiza por medio de una línea vertical a 2 y el tema B por medio de una línea vertical a 1.

Ejemplo 1. Tema A

Ejemplo 2. Término métrico simple A

Ejemplo 3. Término métrico simple B

Ejemplo 4. Término métrico simple C
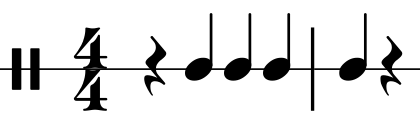
Ejemplo 5. Término métrico simple D

Ejemplo 6. Término métrico compuesto conformado por los términos simples A, B, C y D (esquema material de identidad métrico del Tema A)

Ejemplo 7. Tema B

Ejemplo 8. Términos métricos compuestos conformados por los términos simples A y B (esquema material de identidad métrico del Tema B)
Esta discontinuidad es entretejida por medio de las siguientes operaciones que Beethoven introduce en el propio desarrollo del tema A y en la transición:
I. Desarrollo tema A

Ejemplo 9. Desarrollo del tema A, conformado por la dilatación del término métrico simple D
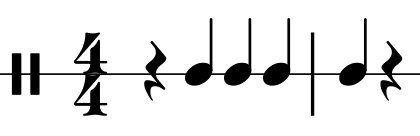
Ejemplo 10. Término métrico simple D

Ejemplo 11. Dilatación del término métrico simple D (esquema material de identidad métrico del desarrollo del tema A)
II. Transición (1)

Ejemplo 12. Transición primera, conformada a partir de la contracción de los términos métricos simples B y C

Ejemplo 13. Esquema material de identidad métrico de la transición primera
III. Transición (2)

Ejemplo 14. Transición segunda, conformada a partir de una combinación entre contracciones y dilataciones de los términos métricos simples B y C
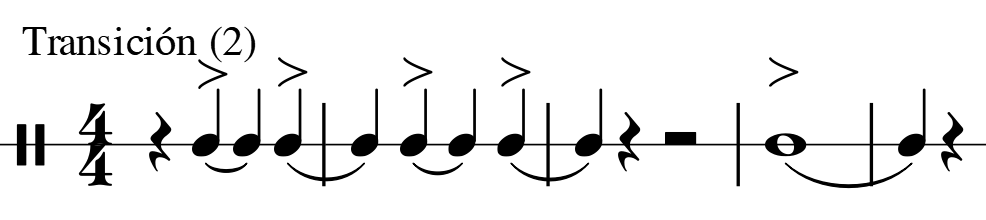
Ejemplo 15. Esquema material de identidad métrico de la transición segunda
IV. Transición (3)

Ejemplo 16. Transición tercera, conformada a partir de una dilatación de los términos métricos simples B y C

Ejemplo 17. Esquema material de identidad métrico de la transición tercera
Como podemos comprobar, después de estas tres grandes periodicidades (junto con el desarrollo del Tema A) que constituyen la transición al Tema B de la Sonata (conformado, a su vez, por la combinación ingeniosa y operatoria de los términos métricos simples expuestos en el Tema A por medio de las contracciones y dilataciones métricas), aparece un enlace de dos compases que métricamente proviene del término métrico simple D; el término que será la base métrica por la que concurrirá y se desarrollará este nuevo tema.
Entrelazamientos melódicos
El entrelazamiento melódico lo podemos observar en los casos donde unas figuras de la dialéctica fuesen impulsadas hacia otras por medio de una identidad melódica que necesitara de ciertos movimientos de entrelazado para no incurrir en un corte discursivo. Puede verse como ejemplo el segundo movimiento de la Sonata “Fácil” de Mozart, a saber;

Ejemplo 18. Tema A

Ejemplo 19. Tema B
¿Cómo se entrelazan ambos temas? A partir de la siguiente variación del tema A:

Ejemplo 20. Variación del tema A
Esta variación está conformada por continuos movimientos melódicos angulares que además, sin perder la identidad del tema A, incorporan una mayor divergencia terminológica en cuanto a cromatismos, floreos y saltos interválicos; Divergencias que darán pie al desarrollo melódico posterior del Tema B en la dominante (metábasis).
Estos entrelazamientos melódicos pueden hallarse en toda la música, por ejemplo; sigamos con la misma Sonata “Fácil”. En el primer movimiento de esta, el tema A y el tema B están entretejidos, principalmente, por los términos métricos simples de las dos semicorcheas del floreo y los términos melódicos simples de las terceras y el semitono, los cuales constituyen los elementos operacionales de la transición que serán conjugados por medio de contracciones, dilataciones, mutaciones y transformaciones.

Ejemplo 21. Tema A

Ejemplo 22. Transición al tema B
Como puede comprobarse, en el compás 9 comienza la transición al tema B, donde Mozart incorpora una transformación al contraer la periodicidad que venía desarrollando para, así, dilatarla hasta la semicadencia en la dominante. Ahora bien, este impulso llevado a cabo por la transformación de la periodicidad (divergencia en progressus) no podría haber sido compensado y entrelazado con el Tema B si no hubiera añadido el compás anterior al inicio de dicho Tema. Este compás sirve de hilo conector que entrelaza definitivamente el Tema A con el Tema B, y que asimila la metábasis lisológica consecuente del impulso de la transformación.

Ejemplo 23. Final de la transición y principio del tema B
Entrelazamientos contrapuntísticos
El mejor ejemplo de entrelazamiento contrapuntístico que podemos encontrar está codificado, como parte esquemática formal, en los divertimentos o episodios modulantes de la fuga. En este sentido no es gratuita la insistencia de los profesores de composición de antaño al otorgar a la fuga una enorme importancia ya que en su esencia reside el dominio del saber hacer, el oficio del entretejimiento contrapuntístico necesario para el desarrollo del arte compositivo. Los entrelazamientos contrapuntísticos pueden desarrollarse por medio del procedimiento técnico de los divertimentos, los estrechos, los pedales de dominante o tónica (principalmente), etc. Véase como ejemplo de un procedimiento de entretejido contrapuntístico, los siguientes ejercicios del libro inédito Apuntes de Contrapunto y Fuga de D. Manuel Massotti Littel:
I. Divertimento

Ejemplo 24. Sujeto de Fuga de M. Massotti Littel

Ejemplo 25. Divertimento de M. Massotti Littel
II. Estrecho

Ejemplo 26. Estrecho de M. Massotti Littel
Entrelazamientos acórdicos
El entrelazamiento acórdico proviene históricamente de la primera especie del contrapunto severo visto desde una perspectiva vertical en la cual se establecen fundamentales e inversiones de éstas que objetivan el propio acorde. La armonía que se estudia en los Conservatorios es (sobre todo ahora) un estudio de los acordes como síntesis armónica basada en un a priori sistemático proveniente del organicismo tonal que se codificó en la Alemania del siglo XIX (el entrelazamiento acórdico es la esencia del coral luterano si bien entendiendo que éste nunca puede ser hipostasiado de su génesis contrapuntística). Así pues, el acorde es en sí una totalidad atributiva conformada por distintas notas (totalidades distributivas) que se entretejen a través de su constitución.

Ejemplo 27. Entrelazamiento del acorde de Do mayor por medio del acorde de de su dominante (Sol)
Entrelazamientos cromatofónicos
Así como el contrapunto y la armonía (desde unas coordenadas basadas en la armonía de Rameau y no desde los improductivos reduccionismos de adecuación organicista de los acordes) son disciplinas que tratan acerca del entretejimiento de las contraposiciones sonoras en un todo compacto desde los términos constituidos en los ejes X e Y; la orquestación o instrumentación es la disciplina que se ocupa de entrelazar los términos constituidos en el eje Z, y, en este sentido, el estudio cromatofónico de la música, en lo concerniente a la intensidad, presión, densidad y amplitud de los sonidos, será el asunto esencial que deberemos tratar en esta especie de entrelazamientos.
Lisológicamente pongamos como caso el Do6 de una flauta en comparación con el Do3 de una tuba. En cuanto a tensión se refiere (tensio = estirado; define las alturas del sonido, eje Y), el Do6 tendría mayor número de vibraciones por segundo que el Do3 por lo que sería más tensivo el Do de la flauta, ahora bien, la presión (comprimire = apretar; relación entre los cuerpos vibrantes respecto al sonido que producen) que debe realizar el tubista para emitir el Do3 es enorme ya que la tuba en esa última tesitura posee gran dificultad en su ejecución. En cuanto a intensidad se refiere (intensus = cualidad de tendido hacia dentro que afecta fuertemente a los sentidos), la flauta sería mucho más intensa debido a que son mucho más perceptibles los sonidos agudos que los graves, además del alto grado de sonoridad de la flauta en dicha tesitura. No cabría hablar de densidad (densus = compactado o condensado de sonidos que establezcan el grosor del volumen sonoro), en este caso, a no ser que la tuba y la flauta emitieran los sonidos a la vez teniendo que compactar los armónicos del uno con el otro. Para analizar en detalle lo concerniente a la densidad, pongamos como ejemplo la morfología de un acorde respecto a otro. Un acorde perfecto mayor puede ser una totalidad atributiva si tomamos como referencia las notas distributivas que forman el acorde, mas si la referencia estriba en el acorde en sí respecto a las múltiples distribuciones tímbricas por las cuales puede establecerse, en ese momento el acorde perfecto mayor será una totalidad distributiva. Así pues, dependiendo de las capas tímbricas que lo forman, podríamos referirnos a mayor o menor densidad del acorde aun siendo contradictorio respecto a su propia tensión, por ejemplo: el acorde de séptima de dominante tiene más tensión que el perfecto mayor por concurrir el primero en mayor número de sonidos que el segundo y, por ende, establecer mayor choque de armónicos; sin embargo, un acorde de séptima de dominante puede establecerse en menor densidad que uno perfecto mayor por estar codificado con una distribución cromatofónica más densa.
Es importante discernir también entre densidad y amplitud. La amplitud se refiere a la distribución interválica de las distintas partes de una partitura de orquesta, de instrumento polifónico o de coro siendo las distribuciones “abiertas” de mayor amplitud (por ejemplo, un acorde perfecto mayor distribuido en Do2 – Do3 – Sol3 – Mi4) y las distribuciones “cerradas” de menor amplitud (Do2 - Sol2 -Do3 - Mi3). En este sentido, una gran amplitud del volumen musical podría orquestarse con mayor o menor densidad (más o menos carga de instrumentos de viento metal, por ejemplo); aquí hallamos otro ejemplo symploké entre las partes del eje Z.
En consecuencia, el equilibrio entre densidad, presión, intensidad y amplitud emergentes de los distintos cromatofonismos de los instrumentos será determinante y esencial en el mundo de la instrumentación donde el entrelazado de las distintas morfologías tímbricas determinará toda la claridad estructural de la expansión de una obra musical.
Periodicidades Interrumpidas
El término “interrupción” está tomado de la clasificación de las cadencias donde la cadencia constituida por una dominante-tónica (esencia del intervalo de quinta), considerada como la Cadencia Perfecta, es interrumpida al no resolver según la propia tendencia del acorde, es decir, por no resolver en una quinta descendente, sino en un grado superior (sexto grado del tono principal que adquiere mayor carácter de interrupción, y por ende de dilatación, si está en modo menor aunque también se considera “rota” a la cadencia sobre el sexto grado mayor). Esta cadencia lleva el nombre de Rota, Engaño o Interrumpida y es de vital importancia debido a que al “romper” el discurso evitando su propia resolución, caída o cierre (cadere = caer) genera una expansión que tomamos como punto de partida de nuestra clasificación. Véase, en primer lugar, un ejemplo de Cadencia Perfecta (V-I) de Do Mayor:
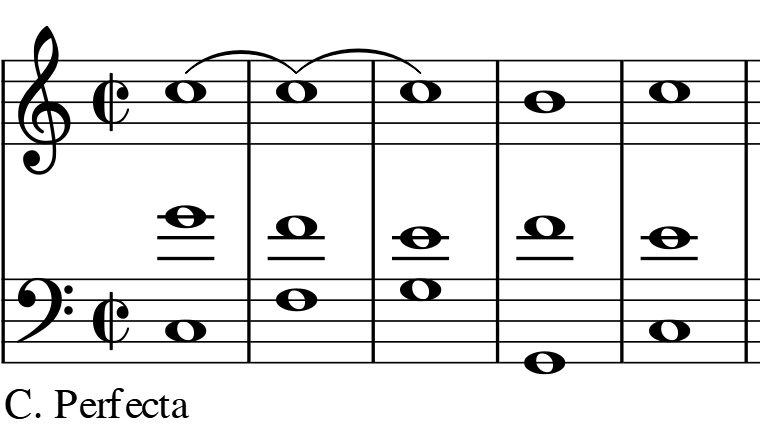
Ejemplo 28. Cadencia perfecta de Do Mayor
Ahora véase este mismo ejemplo, extendido por la Cadencia Rota (V-VI):

Ejemplo 29. Cadencia rota de Do mayor
Como se puede apreciar, al introducir dicha cadencia, la música precisa de una ampliación para asimilar la divergencia que ha supuesto el “romper” con el patrón establecido de la Cadencia Perfecta (V-I). En este sentido, la interrupción no se considerará en sus especies métrica, melódica, contrapuntística, acórdica o tímbrica –al igual que en las anteriores periodicidades– ya que esta periodicidad es en sí una contraposición morfológica que constituye la esencia de las periodicidades dilatadas, contraídas, mutadas, transformadas, etc. La discontinuidad no será considerada como interrupción, así como la dilatación o contracción no son consideradas como mutación si bien están íntimamente imbricadas.
Este ejemplo de interrupción de un patrón lo podemos hallar y analizar en sustantividades más complejas como por ejemplo en el último movimiento de la Octava Sinfonía de Beethoven:
Este movimiento está en la escala diatónica de Fa mayor y alcanza en progressus la modulación a su dominante (Do mayor) en los compases 10 y 11.

Ejemplo 30. Inicio del último movimiento de la Octava Sinfonía de Beethoven
A continuación, del compás 11 al 18, por medio de repeticiones sobre la nota pedal de Do, se produce lisológicamente una catábasis, si bien en el propio compás 18 se interrumpe el discurso debido a un Do# inesperado:

Ejemplo 31. Interrupción del discurso musical con el Do#
¿Qué hubiera pasado si Beethoven no hubiera añadido ese Do #?

Ejemplo 32. Hipotético fragmento del compás 18 sin el Do#
La propia divergencia del Do# abre la longitud de la obra llegando a asimilar dicha divergencia en el compás 380 donde adquiere sentido como función de dominante de Fa# menor (con el La como nota común) por medio de una dilatación. En este sentido, el Do# forma parte de la divergencia más esencial del movimiento que, al asimilarse, conforma la identidad complexa de la obra.

Ejemplo 33. Dilatación del Do# como entrelazamiento de las relaciones entre Fa mayor y Fa# menor
Glomérulos constituidos por periodicidades de compases: periodicidades mutadas y transformadas
Vicente Chuliá FMM 051 (39' 58'')
Glomérulos constituidos por periodicidades mutadas y transformadas
Mutación proviene del latín mutatio y este a su vez del verbo mutare; tanto las palabras “mudar” como “mutar” vienen de dicha etimología. El verbo mutare se desarrolló a partir de la raíz indoeuropea mei-1 –“cambiar y mover”– y del griego amoibe –“cambio”–. En este sentido, toda contracción o dilatación responde a dicho “cambio” o mutación respecto a la identidad original, mas no se incluirán dentro de las periodicidades mutadas debido a su propio isomorfismo constitutivo que cambia en cuanto a longitud de valores métricos y no en cuanto a morfologías en sí. La mutación es un recurso frecuentemente utilizado en las fugas para señalizar un cambio del sujeto (o contrasujeto) en su propia respuesta que, al estar en la quinta del tono principal, debe ajustarse a la perspectiva de progressus, así como a la de regressus una vez retorna al tono principal. Dicho recurso permite el enlace con el siguiente sujeto en el tono principal; ahora bien, desde nuestras coordenadas y observando la importancia de la disciplina del contrapunto en la esencia de la escritura musical, no nos limitaremos solamente a estudiar las mutaciones que concurren dentro de la forma de la fuga, sino todas aquellas que se emplean externamente a ésta en el resto de las formas distributivas de la historia y que, por tanto, clasificaremos en las siguientes especies:
Traslaciones
Son todas aquellas mutaciones del eje Y que, sobre un propio isomorfismo, concurren en algún cambio esencial. Como ejemplo, veamos los siguientes fragmentos:

Ejemplo 1. Concierto nº 6 en La menor para violín de A. Vivaldi

Ejemplo 2. Sujeto de Fuga del Arte de la fuga de J. S. Bach

Ejemplo 3. Sujeto de Fuga sin mutación

Ejemplo 4. Sujeto de Fuga con mutación
Traslaciones
Distinguiremos a la variación como un tipo de mutación que puede concurrir mediante cambios de movimiento; floreos melódicos, apoyaturas, escapadas o notas de paso; cambios modales; así como mediante la armonización o contrapunteo. De las variaciones como periodicidades mutadas nace el esquema formal constituido por un tema y variaciones:

Ejemplo 5. Tema y Variaciones en Do mayor de W. A. Mozart

Ejemplo 6. Primera variación
Movimientos contrarios
Todo movimiento, tema o sujeto que sea reproducido de manera isomorfa, contraída, dilatada, trasladada o variada en el mismo movimiento (ascendente o descendente) a la propia proposición inicial, se denominará movimiento directo; en cambio, cuando la periodicidad inicial se imite a la inversa se denominará movimiento contrario. Véase el siguiente ejemplo:

Ejemplo 7. Movimiento contrario regular
El movimiento contrario será regular cuando los tonos y semitonos se correspondan respecto al modelo siendo lo opuesto movimiento contrario irregular. Si contraponemos a la escala diatónica mayor varias escalas diatónicas distintas por movimiento contrario, veremos que con la única que guarda correspondencia de tonos y semitonos es con la escala de tercera, es decir, aquella en la cual la nota inicial de la escala modelo es imitada por su tercera superior:

Ejemplo 8. movimiento contrario regular (distancia de 3ª)
Esta imitación contraria de dos escalas diatónicas es totalmente regular; de no ser imitada por un intervalo de tercera superior, forzosamente resultaría irregular. De las imitaciones contrarias irregulares en las tonalidades diatónicas, las más usadas son aquellas basadas en las escalas contrarias de quinta u octava:

Ejemplo 9. movimiento contrario irregular (distancia de 5ª)
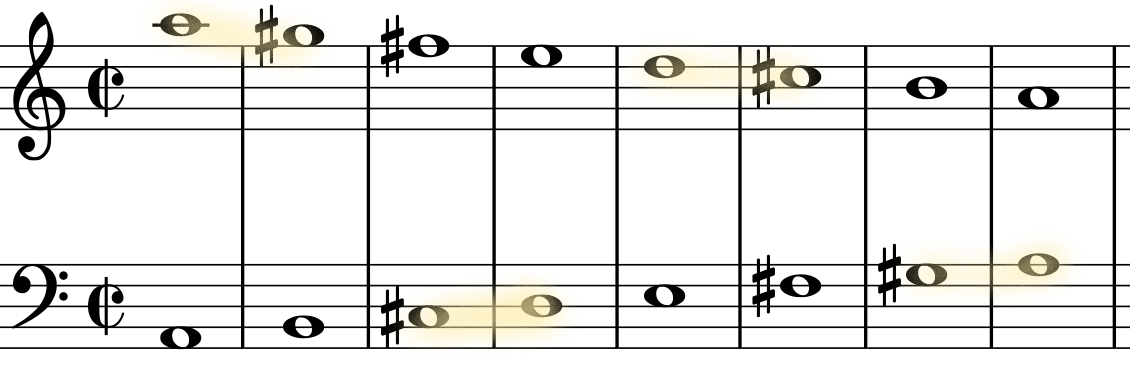
Ejemplo 10. movimiento contrario irregular (distancia de 8ª)
Véase el siguiente ejemplo de imitación por movimiento contrario irregular:

Ejemplo 11. movimiento contrario irregular
En el modo menor, en cambio, la imitación contraria regular es más difícil debido a los distintos modelos de escala menor que concurren según sea ascendente o descendente (natural, armónica, melódica...). Si contraponemos escalas menores a distintos intervalos con la escala modelo de La menor, observaremos que la única que nos lleva a un resultado aproximado en cuanto a la correspondencia de intervalos es la siguiente escala dispuesta a distancia de quinta respecto al modelo y que permite usar indistintamente los grados VI y VII naturales o alterados:

Ejemplo 12
Tan sólo cuando en el motivo no figuren los intervalos correspondientes a los compases 4, 5, 6 y 7 del ejemplo anterior, la imitación contraria en el modo menor a distancia de quinta será totalmente regular:

Ejemplo 13. movimiento contrario regular en La menor
Como puede observarse, aquí yace otra de las razones de la evolución entre las tonalidades formadas por tetracordos eclesiásticos y las tonalidades diatónicas, a saber, las terceras mayores, al ser armónicos más lejanos, permiten la regularidad “natural” del movimiento contrario (divergencia) siendo el movimiento directo de la polifonía primitiva lo “natural” de tales modos, y, por tanto, lo menos proclive a extender la forma musical por medio de la contraposición ejercitada, a excepción de la posterior evolución (música ficta) donde la alteración sirvió de transición entre los tetracordos eclesiásticos con sus respectivos modos y las escalas diatónicas. Este principio de la extensión del diatonismo ya aparece en el libro de Humphrey Searle El contrapunto del siglo XX, a saber:
«Incluso Schoenberg llamaba a su sistema “Composición basada en doce notas referidas exclusivamente la una a la otra entre sí”, significando que, para él hay doce “tonalidades” de igual importancia que requieren ser equilibradas unas con otras. En realidad, detrás de todas las complicaciones, variaciones, comprensiones y elipsis de la música actual, hallamos todavía un centro tonal, naturalmente, no igual a la antigua tónica, y referido ahora a una escala de doce notas, en vez de siete. El sistema diatónico se ha visto substituido por lo que llamo “expansión de la tonalidad”, concepto que espero discutir más detalladamente en los próximos capítulos. En resumidas cuentas, vivimos en un período predominantemente contrapuntístico, en cierto modo paralelo a la época entre Palestrina y Bach; el sistema diatónico de los siglos XVIII y XIX ha cesado de existir en su antigua forma, pero no hay ruptura completa con el pasado; elementos de la antigua música han continuado en la nueva, y poseemos una distinta concepción de la tonalidad, basada en la escala de las doce notas. […] Creo yo, sin embargo, en el libre uso de las doce notas de la escala cromática; creo también que cada conjunto armónico y contrapuntístico posee una fundamental, que puede ser descubierta. Esa fundamental puede continuar por un largo tiempo, y puede cambiar rápidamente; y cuanto más se haga resaltar una “fundamental”, será más tonal la música, y viceversa. “Tonalidad” y “atonalidad” son, de esta forma, sólo cuestiones de grado; no diferencias fundamentales.»{1}
Rotaciones
Rotación proviene del latín rota (rueda) y se refiere a la acción y efecto de dar vuelta. La rotación como mutación periódica se referirá a las imitaciones o contrapuntos retrógrados , “en espejo” o “en cangrejo”, donde el motivo o tema sea reproducido comenzando por el final, esto es, de derecha a izquierda:

Ejemplo 14. Contrapunto retrógrado en la Ofrenda musical de J. S. Bach
Mixtura de especies
Si se analizan detalladamente todos los motivos oídos en una composición idéntica de una obra musical, independientemente de poder aplicárseles todas las periodicidades analizadas anteriormente (isomorfismos, contracciones y dilataciones, entrelazamientos y mutaciones), tambien pueden acontecer mescolanzas o mixturas entre éstos que siempre se darán a nivel morfológico y, por lo tanto, no se establecerán desde especies lisológicas. En los estudios de fuga escolástica se estudia este género de periodicidades como “mutaciones retrógradas contrarias”. Véanse los siguientes ejemplos extraídos del tratado Apuntes de contrapunto y fuga de M. Massotti Littel:

Ejemplo 15. Sujeto de fuga, M. Massotti Littel

Ejemplo 16. Sujeto de fuga, por movimiento contrario

Ejemplo 17. Sujeto de fuga, por movimiento retrógrado directo (rotación)

Ejemplo 18. Sujeto de fuga, por movimiento retrógrado contrario (mixtura entre rotación y movimiento contrario)
Transformaciones
Así pues, una vez explicados todos los recursos que constituyen las especies de mutaciones, hemos de introducir las periodicidades transformadas, aquellas que tienen lugar cuando la escritura compositiva comienza a expandirse aun más a partir de las combinaciones entre el estilo contrapuntístico y el estilo melódico en instituciones como la sonata clásica o la sinfonía. Aquí se hallan los recursos de las mutaciones operados en sentido límite que dan como resultado la expansión en temas donde “lo mismo desarrolla lo distinto y lo distinto desarrolla lo mismo” (metábasis). Como ejemplos, tenemos todos los temas B de todas las sonatas; si las sonatas están bien conformadas, los temas B constituirán o bien una transformación del tema A o de partes del tema A, o bien de la introducción, etc. Véase el siguiente ejemplo de la Sonata “Fácil” de Mozart.

Ejemplo 19. Tema A
Si analizamos este primer glomérulo y lo comparamos con el glomérulo del tema B en la dominante, nos podemos dar cuenta que las identidades A, B y C aparecen en este segundo glomérulo mutadas de tal forma (con rotación de los términos melódicos, contracción de los términos métricos, traslación de los términos armónicos, etc.) que ha pasado a constituir un tema distinto, una transformación en metábasis:

Ejemplo 20. Tema B
En consecuencia, con todo lo explicado en esta clase de glomérulos constituidos por Periodicidades de compases, podemos concluir que a través de toda la pluralidad de géneros y especies de glomérulos, el sujeto operatorio puede disponer de las posibilidades geométricas de poder hacer con sonidos una construcción racional verdaderamente admirable.
Nota
{1} Humphrey Searle, El contrapunto del siglo XX, Vergara, Barcelona 1957, págs. 15 y 183.
 Fundación Gustavo Bueno
Fundación Gustavo Bueno